Minggu, 15 Maret 2015

Volume dalam termodinamika

Volume

Dari Wikipedia bahasa Indonesia, ensiklopedia bebas
olume atau bisa juga disebut kapasitas adalah penghitungan seberapa banyak ruang yang bisa ditempati dalam suatu objek. Objek itu bisa berupa benda yang beraturan ataupun benda yang tidak beraturan. Benda yang beraturan misalnyakubus, balok, silinder, limas, kerucut, dan bola. Benda yang tidak beraturan misalnya batu yang ditemukan di jalan. Volume digunakan untuk menentukan massa jenis suatu benda.

Rumus volume[sunting | sunting sumber]

BentukRumus volumeVariabel
Kubusa^3\;a = panjang sisi/rusuk
Silinder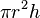\pi r^2 h\;r = jari-jari alas, h = tinggi
Prisma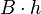B \cdot hB = luas alas, h = tinggi
Balokl \cdot w \cdot hl = panjang, w = lebar, h = tinggi
Prisma segitiga\frac{1}{2}bhlb = panjang dasar segitiga, h = tinggi prisma, l = length of prism or distance between the triangular bases
Bola\frac{4}{3} \pi r^3r = jari-jari bola
dimana merupakan integral luas permukaan bola
Ellipsoid\frac{4}{3} \pi abca, b, c = semi-axes of ellipsoid
Torus(\pi r^2)(2\pi R) = 2\pi^2 Rr^2r = jari-jari kecil, R = jari-jari besar
Limas\frac{1}{3}BhB = luas alas, h = tinggi limas
Limas persegi\frac{1}{3} s^2 h\;s = sisi samping alas limas, h = tinggi
Limas segiempat\frac{1}{3} lwhl = panjang, w = lebar, h = tinggi
Kerucut\frac{1}{3} \pi r^2 hr = jari-jari lingkaran di dasar kerucut, h = jarak dari dasar ke pucuk atau tinggi
Tetrahedron[1]{\sqrt{2}\over12}a^3 \,panjang sisi a
Parallelepiped 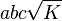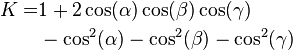a b c \sqrt{K}

\begin{align} K =& 1+2\cos(\alpha)\cos(\beta)\cos(\gamma) \\ & - \cos^2(\alpha)-\cos^2(\beta)-\cos^2(\gamma) \end{align}
a, b, and c are the parallelepiped edge lengths, and α, β, and γ are the internal angles between the edges
Volume benda putar
(dibutuhkankalkulus)		\int_a^b A(h) \,\mathrm{d}hh = dimensi apapun,
A(h) = luasan cross-section tegak lurus terhadap hyang didefinisikan sebagai fungsi posisi sepanjang h. adan b adalah batas integrasi volume putar.
(Berlaku untuk semua bangun jika cross-sectional areanya dapat ditentukan dari h).
Semua benda diputar
(dibutuhkankalkulus)		\pi \int_a^b \left({\left[R_O(x)\right]}^2 - {\left[R_I(x)\right]}^2\right) \mathrm{d}xR_O dan R_I menyatakan fungsi dari jari-jari luar dan jari-jari dalam fungsi, secara berurutan.

Rasio volume untuk kerucut, bola, dan silinder dengan tinggi dan jari-jari sama[sunting | sunting sumber]

Kerucut, bola, dan silinder dengan jari-jari r dan tinggi h
Rumus diatas dapat digunakan untuk menunjukkan bahwa volume kerucut, bola, dan silinder dengan jari-jari dan tinggi sama memiliki rasio 1 : 2 : 3, seperti berikut ini.
Besar jari-jari dianggap r dan tinggi dianggap h (menjadi 2runtuk bola), maka volume kerucut
\tfrac{1}{3} \pi r^2 h = \tfrac{1}{3} \pi r^2 (2r) = (\tfrac{2}{3} \pi r^3) \times 1,
volume bola
\tfrac{4}{3} \pi r^3 = (\tfrac{2}{3} \pi r^3) \times 2,
sedangkan volume silinder
\pi r^2 h = \pi r^2 (2r) = (\tfrac{2}{3} \pi r^3) \times 3.
Penemuan rasio volume bola dan silinder 2 : 3 ditemukan oleh Archimedes.[2]

Volume dalam kalkulus[sunting | sunting sumber]

Pada kalkulus, volume dari sebuah region D dalam R3 adalah integral rangkap tiga dari fungsi konstanta f(x,y,z)=1dan biasanya dituliskan sebagai:
\iiint\limits_D 1 \,dx\,dy\,dz.
Integral volume pada koordinat silinder adalah
\iiint\limits_D r\,dr\,d\theta\,dz,
dan integral volume dalam koordinat bola dituliskan sebagai
\iiint\limits_D \rho^2 \sin\phi \,d\rho \,d\theta\, d\phi .

Satuan volume[sunting | sunting sumber]

Satuan SI volume adalah m3. Satuan lain yang banyak dipakai adalah liter (=dm3) dan ml.
  • 1 m3 = 103 dm3 = 106 cm3
  • 1 dm3 = 1 l
  • 1 cm3 = 1 ml = 1 cc

Volume dalam termodinamika[sunting | sunting sumber]

!Artikel utama untuk bagian ini adalah: Volume (termodinamika)
Dalam termodinamika, volume dari sebuah sistem termodinamika adalah suatu parameter ekstensif untuk menjelaskankeadaan termodinamika. Volume spesifik, adalah properti intensif, adalah volume per satuan massa. Volume merupakanfungsi keadaan dan interdependen dengan properti termodinamika lainnya seperti tekanan dan suhu. Contohnya, volume berhubungan tekanan dan suhu gas ideal melalui hukum gas ideal.

Referensi[sunting | sunting sumber]

  1. ^ Coxeter, H. S. M.: Regular Polytopes (Methuen and Co., 1948). Table I(i).
  2. ^ Rorres, Chris. "Tomb of Archimedes: Sources". Courant Institute of Mathematical Sciences. Diakses 2007-01-02.


Untuk mngetahui lebih jauh tentang Artikel Volume dalam Termodinamika ini
"KLIK LINK DIBAWAH INI"


Diposting oleh di Tidak ada komentar:
Label:

Kapasitas kalor

Kapasitas kalor

Dari Wikipedia bahasa Indonesia, ensiklopedia bebas
Termodinamika
Carnot heat engine 2.svg
Mesin panas klasik Carnot
Kapasitas kalor atau kapasitas panas (biasanya dilambangkan dengan kapital C, sering dengan subskripsi) adalah besaran terukur yang menggambarkan banyaknya kalor yang diperlukan untuk menaikkan suhusuatu zat (benda) sebesar jumlah tertentu (misalnya 10C).











Pengukuran kapasitas panas[sunting | sunting sumber]

Kapasitas panas yang ada pada sebagian besar sistem tidaklah konstan, namun bergantung pada variasi kondisi dari sistem termodinamika. Kapasitas panas bergantung pada temperatur itu sendiri, dan juga tekanan dan volume dari sistem.
Berbagai cara untuk mengukur kapasitas panas dapat dilakukan, yang secara umum dilakukan pada kondisi tekanankonstan atau volume konstan. Sehingga simbol kapasitas jenisnya disesuaikan, menjadi Cp untuk kapasitas jenis pada tekanan konstan, dan CV untuk kapasitas jenis pada volume konstan. Gas dan cairan umumnya diukur pada volume konstan. Pengukuran pada tekanan konstan akan menghasilkan nilai yang lebih besar karena nilai tekanan konstan juga mencakup energi panas yang digunakan untuk melakukan kerja untuk mengembangkan volume zat ketika temperatur ditingkatkan.
Panas jenis spesifik dari suatu zat merupakan molekul yang tidak pada kondisi konstan melainkan bergantung pada temperaturnya. Temperatur pada lingkungan pengukuran yang dibuat biasanya juga ditentukan. Conth dua cara untuk menuliskan panas jenis dari suatu zat yaitu:
  • Air (cair): cp = 4.1855 [J/(g·K)] (15 °C, 101.325 kPa) atau 1 kalori/gram °C
  • Air (cair): CvH = 74.539 J/(mol·K) (25 °C)
Untuk cairan dan gas, penting untuk mengetahui tekanan yang digunakan dalam menuliskan nilai kapasitas panas. Kebanyakan data yang dipublikasikan dituliskan pada kondisi tekanan standar.

Hubungan termodinamika[sunting | sunting sumber]

Energi internal dari sebuah sistem tertutup akan berubah dengan menambahkan panas ke sistem atau ketika sistem melakukan kerja.
{\ \mathrm{d}U = \delta Q + \delta W }.
Untuk kerja sebagai hasil dari perubahan volume sistem:
{\ \mathrm{d}U = \delta Q - P\mathrm{d}V }.
Jika panas ditambahan pada volume konstan:
\left(\frac{\partial U}{\partial T}\right)_V=\left(\frac{\partial Q}{\partial T}\right)_V=C_V.
Jadilah kapasitas panas pada volume konstan, CV.
Untuk kapasitas panas pada tekanan konstan, CP, yang diturunkan dari persamaan perubahan entalpi:
{\ H = U + PV }.
Perubahan pada entalpi dapat dirumuskan dengan:
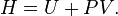
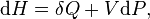
{\ \mathrm{d}H = \delta Q + V \mathrm{d}P },
Sehingga pada tekanan konstan, didapatkan:
\left(\frac{\partial H}{\partial T}\right)_P=\left(\frac{\partial Q}{\partial T}\right)_P=C_P.

Hubungan antara kapasitas panas[sunting | sunting sumber]

!Artikel utama untuk bagian ini adalah: Hubungan antara kapasitas panas
Pengukuran kapasitas panas pada volume konstan seringkali sulit dilakukan pada benda berwujud padat dan cair, karena perubahan temperatur dapat membuat volume zat mengalami pemuaian sehingga membutuhkan penampung yang memiliki kekuatan yang sangat tinggi. Lebih mudah menghitung secara tekanan konstan dan lalu menurunkannya menggunakan persamaan termodinamika dasar.
C_p - C_V = T \left(\frac{\partial p}{\partial T}\right)_{V,N} \left(\frac{\partial V}{\partial T}\right)_{p,N}
Bisa juga dituliskan dengan:
C_{p} - C_{V}= V T\frac{\alpha^{2}}{\beta_{T}}\,
di mana
\alpha  adalah koefisien pemuaian
\beta_T  adalah kompresibilitas isotermal
Rasio kapasitas panas atau indeks adiabatik adalah rasio dari kapasitas panas pada tekanan konstan terhadap kapasitas panas pada volume konstan, yang dapat disebut juga sebagai faktor ekspansi isentropik.

Gas ideal[sunting | sunting sumber]

Untuk gas ideal, mengevaluasi persamaan turunan parsial di atas berdasarkan persamaan keadaan di mana R adalah konstanta gas ideal[1]
p V = R T \;
C_p - C_V = T \left(\frac{\partial p}{\partial T}\right)_{V} \left(\frac{\partial V}{\partial T}\right)_{p}
C_p - C_V = -T \left(\frac{\partial p}{\partial V}\right)_{T} \left(\frac{\partial V}{\partial T}\right)_{p}^2
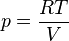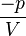
p =\frac{RT}{V }  →\left(\frac{\partial p}{\partial V}\right)_{T}=\frac{-RT}{V^2 } = \frac{-p}{V }
V =\frac{RT}{p } →\left(\frac{\partial V}{\partial T}\right)_{p}^2=\frac{R^2}{p^2}
Substitusikan
-T \left(\frac{\partial p}{\partial V}\right)_{T} \left(\frac{\partial V}{\partial T}\right)_{p}^2 = -T\left(\frac{-p}{V }\right) \left(\frac{R^2}{p^2}\right)=R
Sehingga akan didapatkan persamaan Mayer jika direduksi
C_p - C_V = R

Kapasitas panas spesifik (panas jenis)[sunting | sunting sumber]

Kapasitas panas spesifik (atau panas jenis) adalah kapasitas panas per basis massa
c={\partial C \over \partial m},
di mana pada ketiadaan transisi fase zat akan didapatkan panas jenis:
c=E_ m={C \over m} = {C \over {\rho V}},
di mana
C adalah kapasitas panas
m adalah massa zat
V volume zat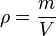
\rho = \frac{m}{V} massa jenis zat
Untuk gas dan bahan lainnya yang berada pada tekanan tinggi, terdapat perbedaan nilai panas jenis pada kondisi yang berbeda. Kapasitas panas dapati didefinisikan dengan measukkan kondisi proses isobarik (tekanan konstan, dp = 0) danproses isokhorik (volume konstan, dV = 0). Hubungan panas jenisnya dapat dirumuskan dengan:
c_p = \left(\frac{\partial C}{\partial m}\right)_p,
c_V = \left(\frac{\partial C}{\partial m}\right)_V.
Sesuai dengan persamaan sebelumnya:
c_p - c_V = \frac{\alpha^2 T}{\rho \beta_T}.

Untuk mngetahui lebih jauh tentang Artikel Kapasitas kalor. "KLIK LINK DIBAWAH INI"
https://id.wikipedia.org/wiki/Kapasitas_kalor

Diposting oleh di Tidak ada komentar:
Label:
Langganan: Komentar (Atom)